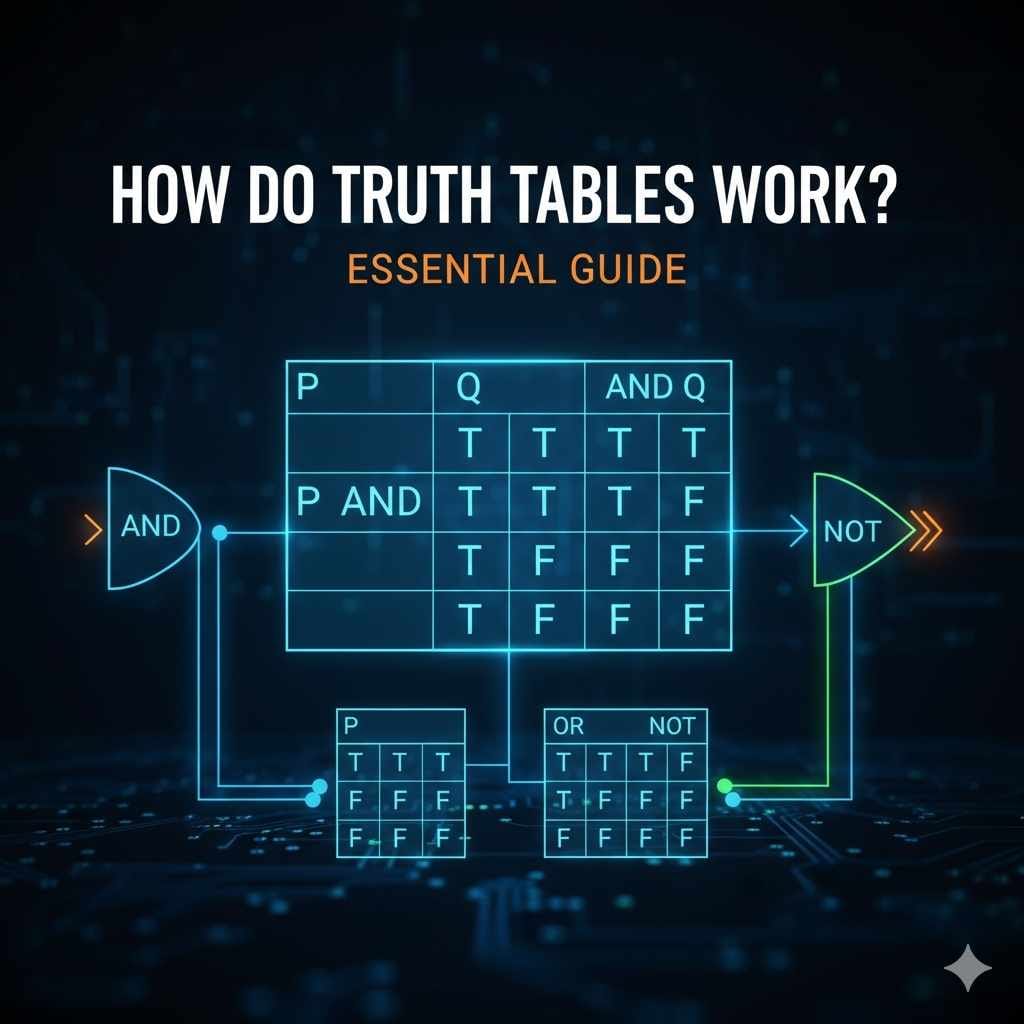
Truth tables are simple charts used in logic and digital systems to map out every possible input combination for a given statement or circuit and show the resulting output. They work by systematically listing all true (T/1) and false (F/0) scenarios to predict behavior reliably, making complex logic easy to check.
When you look at car wiring diagrams or try to understand how a simple switch controls your headlights, things can look confusing fast. Digital logic, which runs everything from your engine computer to your infotainment system, uses the same kind of clear rules. Many people hear the term “truth table” and think it sounds like advanced math, but it’s actually one of the clearest tools we have. If you’ve ever felt lost trying to figure out if a circuit will work, this guide is for you. We will break down exactly how truth tables work, using easy language, so you can understand the logic behind everything from a simple garage light to the brains of your car. By the end of this guide, you will feel confident reading and creating these essential logic charts.
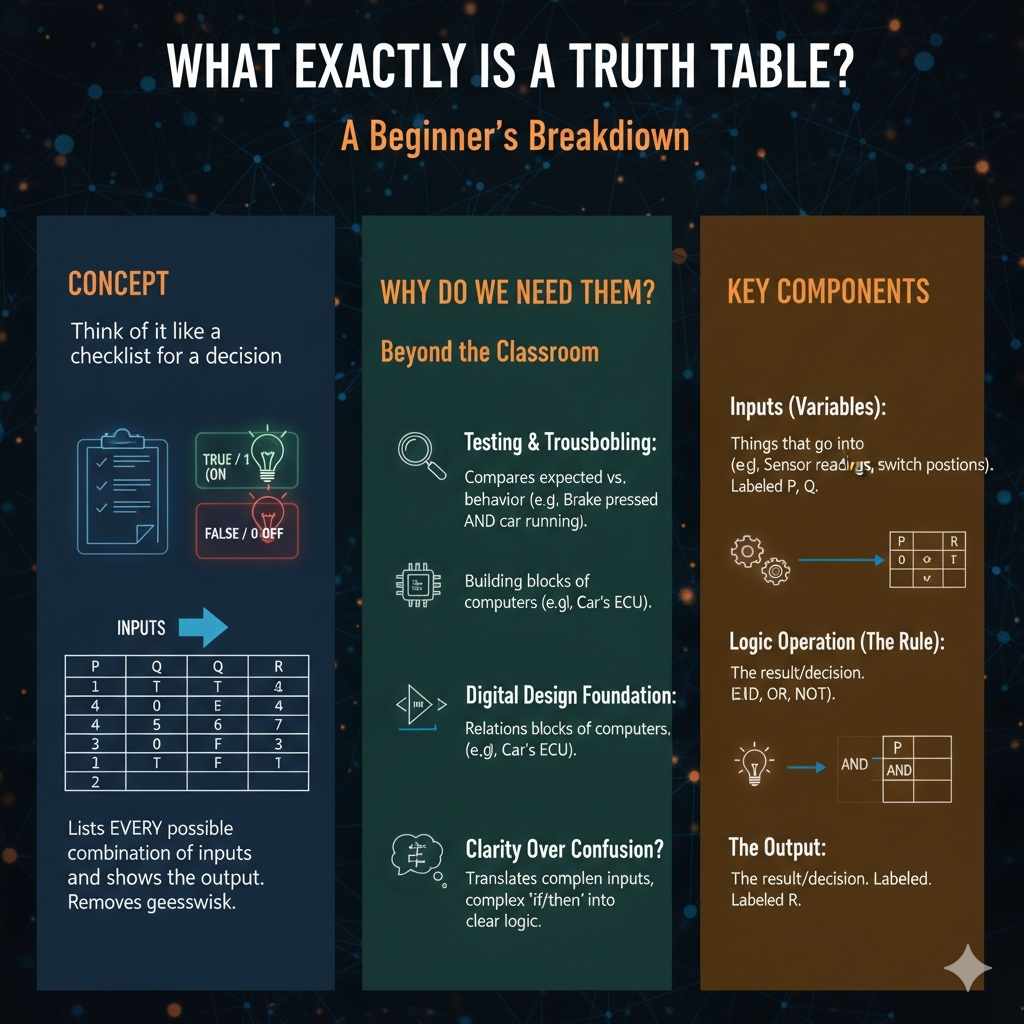
What Exactly is a Truth Table? A Beginner’s Breakdown
Think of a truth table like a complete checklist for a decision. In the world of logic—whether we are talking about making decisions in everyday life or designing the computer chips in your car—we deal with two main states: True or False. In digital electronics, we often call these 1 (On/True) or 0 (Off/False).
A truth table is simply a table that lists every possible combination of inputs and shows what the output will be for each one. It removes all the guesswork. Instead of just hoping a circuit does what you expect, the truth table proves it. This is how engineers guarantee that the complex systems in modern vehicles operate safely and correctly.
Why Do We Need Truth Tables? (Beyond the Classroom)
You might wonder why these charts are so important if you aren’t building microprocessors in your garage. While you might not build them from scratch, understanding them helps you understand how devices work:
- Testing and Troubleshooting: If a car feature isn’t working—say, the brake lights only flash sometimes—a truth table helps compare the expected behavior with the actual behavior under every possible condition (e.g., brake pressed AND car running, brake pressed AND car off).
- Digital Design Foundation: Every logic gate (the building blocks of computers) is defined by a truth table. Understanding these basic gates is the first step to understanding how your car’s Electronic Control Unit (ECU) processes information.
- Clarity Over Confusion: It takes complicated “if/then” statements and lays them out cleanly.
Key Components: Inputs, Outputs, and Logic Gates
To build a truth table, you only need three things:
- Inputs (Variables): These are the things that go into the decision. In a car context, these could be sensor readings, switch positions, or signals. We label these with letters, like P and Q.
- The Logic Operation (The Rule): This is the relationship between the inputs. This is the “how” of the logic. Common operations include AND, OR, and NOT.
- The Output: This is the result, or the decision made after applying the rule to the inputs. We label this R.
The Building Blocks: Understanding Basic Logic Operations
Before we build the chart, we must understand the basic rules of logic. These rules, often represented by electronic components called logic gates, define how inputs combine.
1. The AND Operation (The Gatekeeper)
Think of the AND operation like needing two keys to start an older car: you need Key A AND Key B to be present for the car to start (Output is True).
Rule: The output is True (1) ONLY IF all inputs are True (1).
2. The OR Operation (The Backup Plan)
The OR operation is like having two ways to turn on your interior dome light: you can open the door OR you can flip the switch. If either one is true, the light comes on.
Rule: The output is True (1) IF at least one input is True (1).
3. The NOT Operation (The Inverter)
The NOT operation is the simplest. It just flips the input. If the input is True, the output is False, and vice versa. This is like a safety switch that is normally on, but when you activate it, it shuts something down.
Rule: The output is the opposite of the input.
Step-by-Step: How to Construct a Basic Truth Table
Let’s walk through building a truth table for the simplest logic gate: the two-input AND gate. This shows you the exact process you would follow every time.
Step 1: Determine the Number of Inputs
The first thing you need to know is how many variables (inputs) you are working with. Let’s say we have two inputs, P and Q, for our AND operation.
Step 2: Calculate the Number of Rows Needed
This is a crucial step for efficiency. The number of possible combinations (rows) is calculated using a simple formula: $2^n$, where ‘n’ is the number of inputs.
In our example with 2 inputs (P and Q), $n=2$.
Total Rows = $2^2 = 4$ rows.
If you had three inputs (A, B, C), you would need $2^3 = 8$ rows.
Step 3: Systematically Fill in the Input Columns
This step must always be done the same way to ensure you don’t miss any combination:
- Start with the rightmost input column (Q). Alternate between 0 and 1 for every row (0, 1, 0, 1).
- Move to the next column to the left (P). Alternate between blocks of 0s and 1s, with each block being half the total number of rows. Since we have 4 rows, the pattern is two 0s followed by two 1s (0, 0, 1, 1).
If we had 4 inputs (A, B, C, D, needing 16 rows), the pattern would be:
- D: 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0
- C: 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1
- B: 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1
- A: 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1
This systematic counting ensures that every unique combination is represented exactly once.
Step 4: Determine the Output Column Based on the Logic Rule
Now we apply the rule for the operation we chose (AND, OR, etc.) to the inputs of each row to find the output (R).
For the Two-Input AND table (P AND Q = R): Remember the rule: Output is 1 only if P is 1 AND Q is 1.
| P (Input 1) | Q (Input 2) | R (P AND Q) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
See how that works? Row 4 is the only one where both P and Q are true (1), so the output R is true (1). This table perfectly describes the behavior of an AND logic gate.
Exploring Common Logic Gates with Truth Tables
Let’s build the tables for the other essential operations you’ll encounter when looking at vehicle diagnostics or simple logic puzzles.
The OR Gate Truth Table
Rule: Output is 1 if P is 1 OR Q is 1 (or both).
| P (Input 1) | Q (Input 2) | R (P OR Q) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Notice that the only time the output (R) is 0 is when both P and Q are 0. This is the key difference from the AND gate.
The NOT Gate Truth Table
The NOT gate only has one input (P) and one output (R). It simply inverts the state.
| P (Input) | R (NOT P) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Combining Gates: Complex Logic Operations
Real-world systems often combine these basic operations. For instance, you might need an output that is true only if P is true AND Q is NOT true. This is written logically as $P text{ AND } (text{NOT } Q)$.
To solve this, we build the table step-by-step, creating intermediate columns for each part of the expression:
| P | Q | NOT Q | P AND (NOT Q) |
|---|---|---|---|
| 0 | 0 | 1 | 0 (0 AND 1) |
| 0 | 1 | 0 | 0 (0 AND 0) |
| 1 | 0 | 1 | 1 (1 AND 1) |
| 1 | 1 | 0 | 0 (1 AND 0) |
By breaking the complex problem into smaller pieces (like calculating the ‘NOT Q’ column first), the final result becomes clear. This systematic approach is powerful for debugging anything from simple automotive relay circuits to advanced engine management systems.
Practical Application: Truth Tables in Automotive Systems
While the examples above use 0s and 1s, in your car, these often represent real-world conditions. Understanding how these tables translate helps you approach repairs with more confidence.
Example: Simple Indicator Light Circuit
Imagine a warning light on your dashboard that should only illuminate if two specific conditions are met: the engine is running (P) AND the oil pressure is low (Q). If the engine isn’t running, the light must never come on, regardless of the oil pressure sensor.
This is a perfect scenario for an AND gate. P = Engine Running (1=Yes, 0=No). Q = Oil Pressure Low (1=Yes, 0=No). R = Warning Light On.
| P (Engine Running) | Q (Oil Low) | R (Warning Light On) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
If you are troubleshooting and the engine is running (P=1) but the oil is low (Q=1), yet the light R does not turn on, you know immediately that the logic circuit or the wiring associated with the AND operation has failed. You are looking for a broken connection where the ‘1’ result should be.
Truth Tables and Digital Safety Standards
Safety systems rely entirely on this predictable logic. For instance, the National Highway Traffic Safety Administration (NHTSA) sets standards for vehicle electronics that must be verified using formal methods, including truth tables, to ensure fail-safe operations. When engineers design systems, they must prove that under no combination of inputs will the system produce an unsafe output. You can learn more about the rigorous standards required for vehicle safety systems by reviewing resources from organizations dedicated to transportation safety, like those available through the U.S. Department of Transportation.
Why Readability Matters: Decimal vs. Binary
So far, we’ve used 1s and 0s (Binary). This is the language of computers. However, when you look at a truth table with many inputs, it helps to see the decimal equivalent.
For a 3-input table (A, B, C), the rows represent the numbers 0 through 7 in binary:
| Row Number (Decimal) | A | B | C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 |
If you see a truth table structure, recognize that the input columns are just binary counting systems. If you see 8 rows, it means the inputs are cycling through every number from 0 to 7.
Advanced Topics Made Simple: XOR and XNOR
As you get more familiar with logic, you’ll see two more common gates that mix the AND and OR concepts.
1. Exclusive OR (XOR)
The XOR gate means the output is true only if the inputs are DIFFERENT. It means one or the other, but NOT both.
Think of it like: “Do I have gas OR do I have a charged battery, but not both dead scenarios?”
| P | Q | R (P XOR Q) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Key takeaway: The output is only 1 when the inputs do not match.
2. Exclusive NOR (XNOR)
The XNOR gate is simply the inverse of XOR. The output is true only if the inputs are the SAME (both 0 or both 1).
| P | Q | R (P XNOR Q) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
XNOR gates are often used in systems that need to confirm that two signals are identical, ensuring synchronization.
Putting It All Together: From Table to Circuit Diagram
The goal of building a truth table is often to design or verify an electronic circuit. Every row in the truth table corresponds to a specific part of the circuit working, or not working.
How to Convert a Truth Table Back to Logic Statements
If you are given a complex truth table and asked to figure out what it represents, you look only at the rows where the output (R) is TRUE (1). These are the conditions that cause the output.
Let’s use the table for $P text{ AND } (text{NOT } Q)$ again:
| P | Q | P AND (NOT Q) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 <– Condition 1 |
| 1 | 1 | 0 |
The output is only 1 in Row 3. In Row 3, P is 1 and Q is 0. To state this condition using logic symbols:
When P is True (1) AND Q is False (0), the output is True.
This translates directly to the logic statement: $P text{ AND } (text{NOT } Q)$.
The Sum of Products (SOP) Method
For very complex tables, the official method is called Sum of Products (SOP). You create an expression for every row where the output is 1, linking the inputs with ANDs, and then join all those products with ORs.
If you had three inputs (A, B, C) and the output (R) was 1 in rows 1, 4, and 7:
- Row 1 (001): $(text{NOT } A) text{ AND } (text{NOT } B) text{ AND } C$
- Row 4 (100): $A text{ AND } (text{NOT } B) text{ AND } (text{NOT } C)$
- Row 7 (111): $A text{ AND } B text{ AND } C$
The full SOP expression would be:
$R = [(text{NOT } A) text{ AND } (text{NOT } B) text{ AND } C] text{ OR } [A text{ AND } (text{NOT } B) text{ AND } (text{NOT } C)] text{ OR } [A text{ AND } B text{ AND } C]$
While this looks complicated, remember: you are just listing every scenario that turns the final light on. Truth tables provide the foundation for simplifying these complex expressions later on, though that simplification step is often best left to specialized software for modern vehicle ECUs!
Why This Matters to You as a Driver
You might be thinking, “Dustin, this is logic, not changing my oil.” Here is where it hits home:
- Understanding Error Codes: When your Check Engine Light comes on, the computer is executing millions of these tiny logic checks per second. An error code points to a failure in one of these logic paths (e.g., a sensor reading is stuck at 0 when it should be fluctuating).
- Smart Repairs: If a mechanic tells you that a specific relay needs to be swapped because of a “logic fault,” knowing that logic relies on truth tables means you understand they are checking if the expected true/false combination is occurring.
- DIY Confidence: If you are working with aftermarket lighting or adding auxiliary features to your car, you must wire your switches correctly. Using a simple AND or OR logic based on a truth table ensures your new accessory only turns on exactly when you intend it to, saving you from shorts or melted wires.
Treating your vehicle systems as predictable logic puzzles makes troubleshooting less frustrating and more systematic. Remember, electronics follow strict rules; the truth table shows you those rules clearly.

Frequently Asked Questions (FAQ) About Truth Tables
Q1: Is a truth table the same as a Boolean expression?
No, they are related but different. A Boolean expression (like $P + Q$) is the mathematical shorthand for the rule. The truth table is the complete chart that proves what that expression does under every single possible input condition.
Q2: How do I know whether to use 0 or F, and 1 or T?
It depends on the context. In formal logic study, T (True) and F (False) are common. In electronics and computer science, 1 (High voltage/On) and 0 (Low voltage/Off) are standard. For beginners, pick one convention (like 1 and 0) and stick to it throughout your work for consistency.
Q3: If I have four inputs, how many rows are in my truth table?
You use the formula $2^n$, where $n$ is the number of inputs. For four inputs, it is $2^4$, which equals 16 rows. This covers every single possibility.
Q4: What is the hardest part about building a truth table?
The hardest part for beginners is systematically filling in the input columns correctly without repeating or skipping combinations. Always start by alternating 0 and 1 on the far right, then double that pattern for the next column to the left (two 0s, two 1s, etc.).
Q5: Do I need to know advanced math to use truth tables?
Absolutely not! Truth tables rely on very simple arithmetic (counting in binary) and understanding basic rules like AND, OR, and NOT. The power comes from the structure, not complex calculations.
Q6: Where might I see these logic rules used outside of electronics?
Truth tables are used in contract law to check conditions, in database queries to combine search criteria (e.g., “Find records where Age > 30 AND State = CA”), and in any situation that requires defining precise decision criteria.
Conclusion: Logic Is Your Friend
Learning how truth tables work strips away the mystery from complex digital systems. You now know that every time your car’s computer makes a decision—whether to fire an injector, illuminate a dashboard light, or manage your cruise control—it is running through combinations that could easily be charted in one of these simple, powerful tables.
The key takeaways are consistency and systematic counting. If you have ‘n’ inputs, you need $2^n$ rows. You fill those rows by alternating 0s and 1s, doubling the pattern as you move left. Then, you apply the specific logic rule (AND, OR, XOR) to generate the final output.
Don’t let the charts intimidate you. They are simply your roadmap to understanding system behavior. Whether you’re checking a fuse box schematic or just trying to build a better backup light system on your truck, mastering the truth table gives you the foundational language of reliable design. Keep practicing those basic AND/OR scenarios, and you’ll find that debugging circuits and understanding modern technology becomes much more straightforward and even kind of fun. You’ve got this!